Pages

Construction of a Sundial at Dr. Francisco Sanches Basic School - PT

  •   

     

    Introduction

    Imagine that you have just got the latest in digital watches but, for some reason, maybe a solar storm, any kind of devices works. However, if the sun is shining you don't need to use a watch at all, because the sun makes an excellent clock which (fortunately) doesn't need batteries that can run down. This article is all about a particular kind of sundial and how we can build one for ourselves.

     

    IMPORTANT SAFETY ADVICE

    Never look directly at the sun!

     

    We often take the problem of telling the time or of finding the day's date for granted, but finding solutions to both of these questions is vital to our civilisation. Early men and women needed to have an accurate notion of the seasons in order to know when to plant and harvest their crops. As civilisation developed it became important to know the time during the day. Two times were obvious as everyone was aware of when the sun rose (dawn) and when it set (dusk). More accurate observations of the sun then showed that having risen in the East, it climbed to its highest point in the sky (due South in the Northern hemisphere) before descending towards its setting point in the West. The time of the highest point reached by the sun (which is when the shadows were shortest) is called Noon. Knowing dawn, Noon and dusk gave us morning, afternoon and night.

    Every civilisation has been interested in the way the sun moves, and astronomy and mathematics have always developed alongside each other. Better observations called for quicker and more efficient mathematical methods. More detailed theory drove people to make more accurate observations. In this way both theory and practice evolved together.

    We choose initially not to give too much justification for the mathematics behind the construction of this dial.

    Note that the following article assumes that you are in the Northern Hemisphere. If you want to build a sundial that is to work South of the equator you will need to make some changes, but the following method is easy to adapt.

     

    What is an analemmatic sundial?

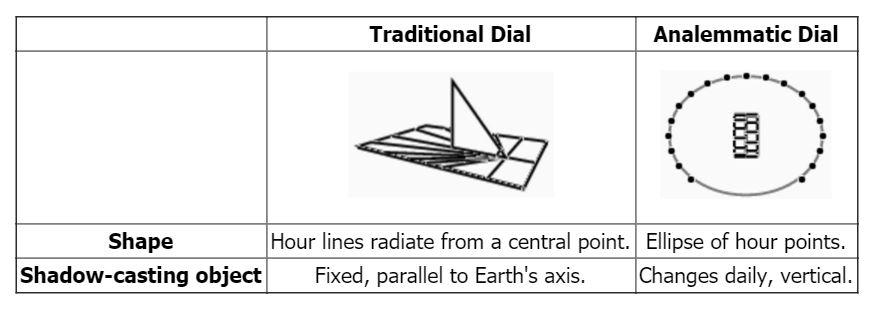
    An analemmatic sundial is a particular kind of horizontal sundial in which the shadow-casting object is vertical, and is moved depending on the date, or to be more precise, depending on the declination of the sun on a given day. The time is read from the dial by noting where the shadow cast by the vertical pin crosses hour points laid out on an ellipse. If we make the dial on the ground and large enough, we can use the shadow cast by a person. This makes it very different from the traditional sundial we see often in parks and gardens where the shadow is cast by a triangular shaped wedge. 

    The ellipse

     

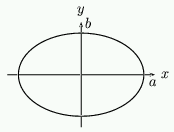
    Figure 5: An ellipse.

    Figure 1: An ellipse.

    As ellipses play such an important role in understanding the analemmatic sundial, we include a short discussion on their theory here. An ellipse is an example of a curve called a conic section. Other conic sections are the circle, the parabola and the hyperbola. The Earth travels around the sun on an elliptical path.

     

    If the points on an ellipse have coordinates (x, y) then x and y are related by the formula:

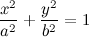
    If a=b then this is simply a circle.

     

     

    What is the declination of the sun?

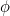    Before we can construct our dial we need to understand what the "declination of the sun" is. Look at figure 1, showing the Earth as seen from the side. Imagine you are standing on the surface of the Earth at the point $P$. Your latitude, i.e. your angular distance from the equator, is marked as $\phi $. The diagram shows the situation at Noon so the sun is at its high point for the day and will appear to be due South from where you stand.

     

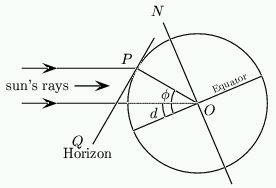
    Figure 1: Calculating the declination of the sun.

    Figure 2: Calculating the declination of the sun.

     

     Using this diagram, show that the angle 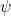$\psi $ that the sun makes with the horizontal at Noon is :

     

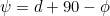
    \begin{equation} \psi = d + 90 - \phi \end{equation}

     

     

    On any given day the declination of the sun, marked as d in figure 1, is the angle the rays of the sun make with the plane of the equator of the Earth. Because the axis of the Earth is tilted and we rotate around the sun, this angle changes during the year. It is this change that gives us the seasons.

    In the Northern hemisphere, d is positive in summer, and at the spring and autumn equinoxes the sun is directly overhead at the equator at Noon so d = 0º . At the summer solstice d = 23.5º, and at the winter solstice d = -23.5º. As the latitude of the equator is 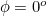$\phi =0^ o$ the formula 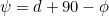$\psi = d + 90 - \phi $ above gives d = 0º.

     

    The path that the sun appears to trace in the sky during the day is a circle. Of course part of this circle will be below the horizon during the night! The centre of this circle is a point due North at an angle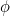$\phi $to the horizontal.

     

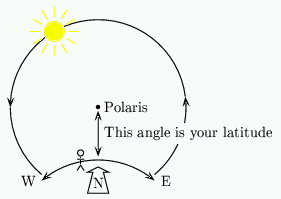
    Figure 3: The path of the sun.

    Figure 3: The path of the sun.

     

    This point is marked (to a very good approximation) by the pole star Polaris. The angle between the sun and Polaris is simply 90º - d.

    In a normal sundial, a shadow is cast by a "gnomon" or pointer that points directly towards Polaris. If a disc of card is stuck to this pointer, perpendicular to it, then the shadow cast by the sun is of constant length throughout the day and moves around the card clockwise with the end point of the shadow lying on a circle. Such a sundial (called an equatorial sundial) is very easy to make and you can see one in figure 2. By seeing where the shadow falls we can tell the time.

     

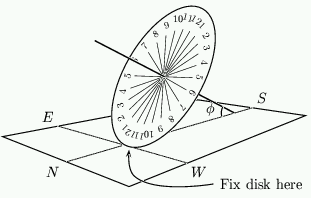
    Figure 4: The completed equatorial sundial.

    Figure 4: The completed equatorial sundial.

     

    In an analemmatic sundial the pointer is vertical. The shadow cast by the sun on a horizontal surface, such as the ground, moves clockwise around the pointer, but this time it varies in length during the day. The endpoint of the shadow no longer falls on a circle. Indeed, when the sun sets, the shadow is of infinite length. We can still tell the time from the position of the shadow, but it is a little more complicated.

     

     

    How does an analemmatic sundial work?

    We said earlier that the end of a pointer, pointing at Polaris, casts a shadow that moves round a circle on a disk parallel to the equator of the Earth. To remind yourself of this setup have a quick look back at figure 4. The sun appears to move around the star Polaris in a large circle. At the equinox when d = 0º this circle is exactly the celestial equator. We can describe the position of the sun by its angle relative to some fixed reference point. For convenience we take this point to be Noon, at which time the sun is highest. 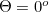The angle $\Theta $ of the sun relative to the Noon point is called the hour angle, with$\Theta =0^ o$ at Noon. In fact 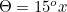$\Theta =15^ ox$, where $x$ is the time (in hours) past Noon.

     

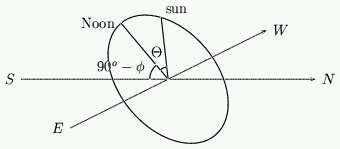
    Figure 14: Finding the hour angle.

    Figure 5: Finding the hour angle.

     

    Now, what shape do we get if we look at the shadow cast by a vertical pointer onto a horizonal surface? To answer this we have to project the circle that the sun makes. If d = 0 this circle is at an angle of 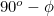$90^ o-\phi $ to the horizontal and intersects the horizontal at 6am and 6pm.

     

    How big should I make an analemmatic sundial?

     

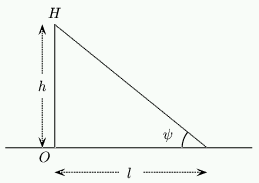
    Figure 7: The height of a person.

    Figure 6: The height of a person.

    We will assume that the sundial is to be constructed outside in a garden and the shadow casting object is to be a person who will stand on the dial itself. Have a look at the diagram on the left. The solid line OH represents a vertical object (a person) which we will assume has length h. The dotted lines are the rays from the sun.

    Using this diagram and equation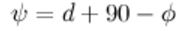show that if the declination of the sun on a given day is d then the length l of the shadow cast by the person at Noon is given by:

     

     

     

    Catarina Gonçalves, Diana Oliveira, Hélio Pires, Lucas Esaú, Miguel Silva, Sara Miranda