How did Eratosthenes measure the circumference of the Earth, a long time before modern technologies period ?
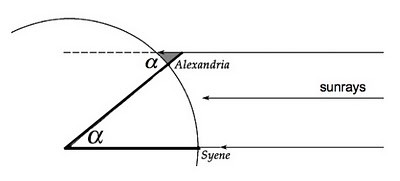
To calculate the Earth circumference, an Ancient Greek mathematician called Eratosthenes went to Syenne in Egypt at the summer solstice. At the summer solstice, sunbeams are perfectly perpendicular to the surface of the Earth in Syenne, close to the Tropic of Cancer. Further, 800 km due North in Alexandria, he saw that the angle of the shadow of an obelisk was 7,2 degrees.
As sunrays are considered parallel, and thanks to the properties of Z-angles, he deduced that the angle between Alexandria and the centre of the Earth and Syene was also 7,2 degrees.
credits http://www.msnbc.com/rachel-maddow-show/
Eratosthenes understood that 7,2 degrees from the center of the Earth corresponds to 800km on the surface of the earth. So he used proportionality rules and multiplied 800km by 360 degrees and divided it by 7,2 degrees.
The circumference of the Earth corresponded to approximately 40 000 km.
Olivier and Hassan
ERASTOTHENES EXPERIMENT IN PALEKASTRO, CRETE
On Monday 21st March, day of the spring equinox, the weather was lovely and it was warm, the sun was shining. The sun rays at the equinox are perpendicular to the equator. We were in Palekastro Primary School in Crete. That day, we calculated the Earth’s circumference using the inclination of solar rays.
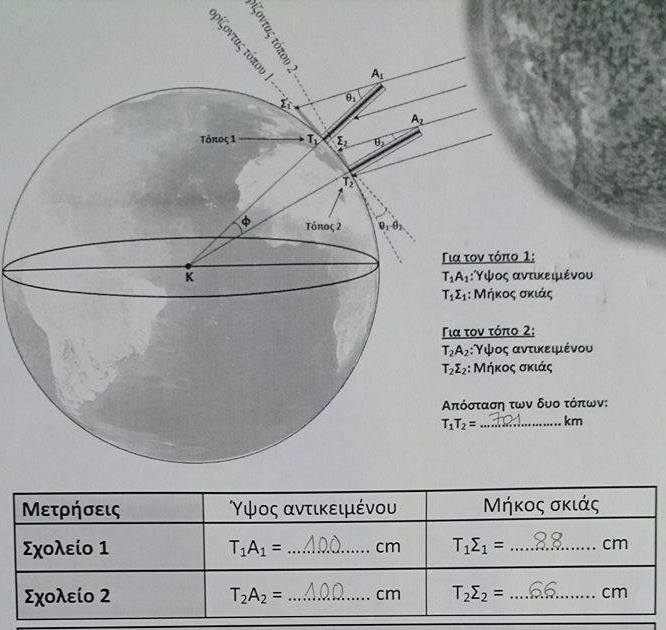
First we took a gnomon 1 m high and with a big ruler we measured the shadow of the gnomon. The shortest length we found was 66 cm, corresponding with solar noon.
At the same time, in another city Didimotichon, located on the same meridian, another school made the same experiment. They measured shortest the shadow and found 88 cm.
The distance between the two cities is 701 km.
|
Right triangles
|
Palekastro
|
Didimotichon
|
Angles
|
|
A1∑1T1
|
T1A1 = 100 cm
|
T1∑1 = 88 cm
|
41,3 °
|
|
A2∑2T2
|
T2A2 = 100 cm
|
T2∑2 = 66 cm
|
33,4 °
|
We calculated the angle the sun rays were making with the gnomon.
In the right triangle ∑1A1T1 :
Tan (O1) = ∑1T1/T1A1 = 88/100 = 0,88
Therefore, O1 = arctan (0,88) = 41, 3°
In the right triangle ∑2A2T2 :
Tan O2 = ∑2T2/T2A2 = 66 /100 = 0,66
Therefore O2 = arctan (0,66) = 33,4°
41,3°- 33,4° = 7,9 °
7,9°corresponds to 701 km therefore, by cross product, 360°correspond to 31 944,3 km.
The circumference of the Earth we found is 31 944, 3 km.
ERATOSTHENES EXPERIMENT IN REUNION ISLAND-22nd MARCH 2016
We did the Eratosthnes experiment in Reunion Island on the 22nd March 2016, the day after the equinox, at solar noon, 12:23 (local time)when the sunbeams are perpendicular to the Equator.
Instead of an obelisk, we used a 1 meter high ruler and measured the length of the shadow.
We had no other school to work with that day, so we refered to a point on the equator at the same longitude (55°3 E). The angle sunbeams make with the ruler should be almost 0° because we were just the day after the equinox.
Distance between the two places : 2325 km called D.
So, we did the experiment:
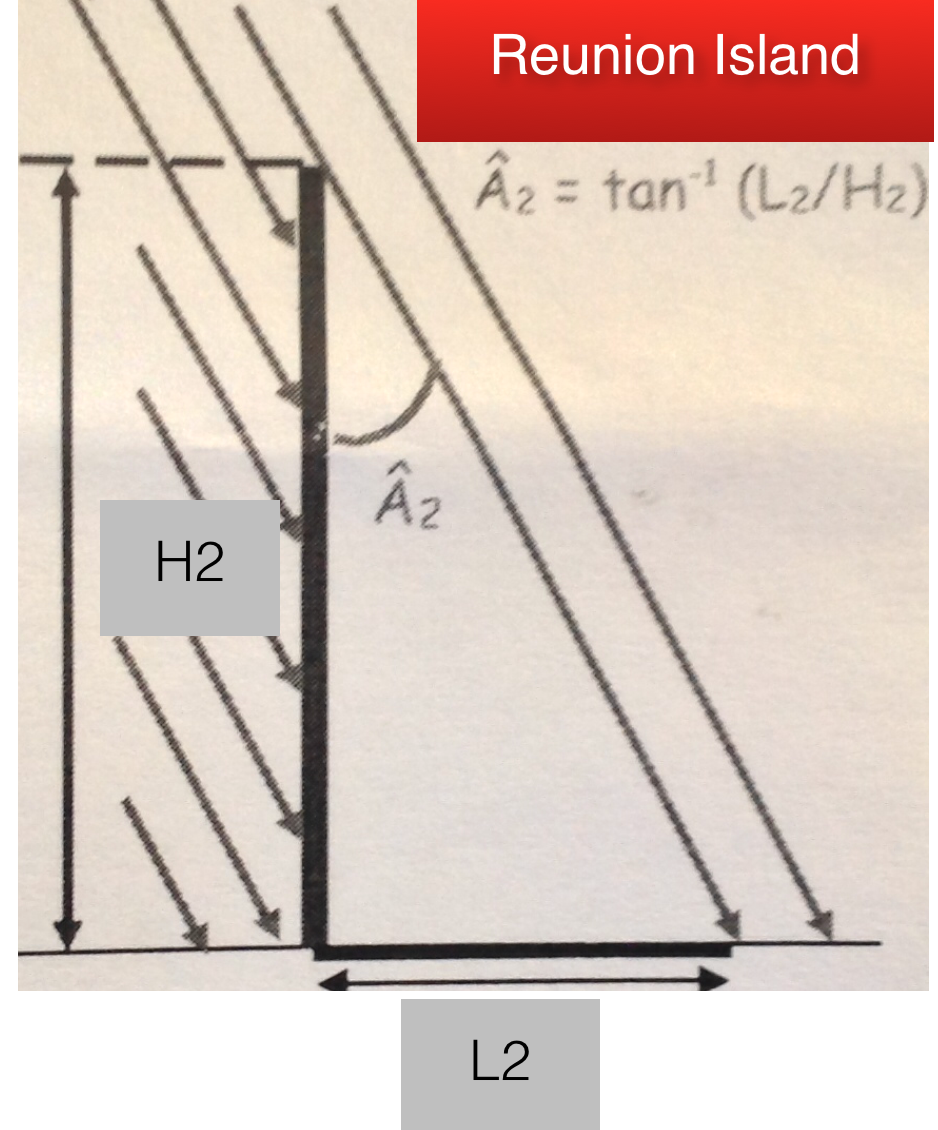
The length of the shadow at 12:23 was in Reunion Island : 0,41m ; we called it L2. H2 is the height of the ruler : H2 = 1
We had to find the angle A2. We found it by trigonometry (here the tangent of an angle in a right angled triangle) :
So we have: A1 = 0 ° and
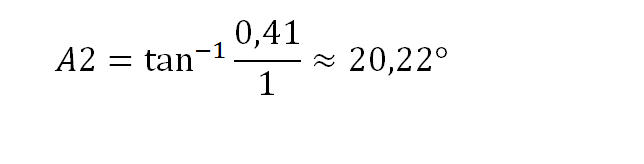therefore
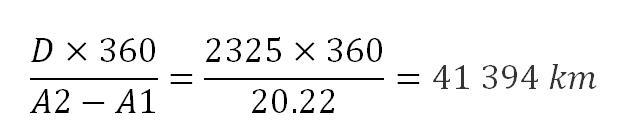
The result is approximately the same as Eratosthenes found but not very accurate because the Earth is lightly flattened at the poles more than spherical.
Hassan and Olivier
Inspirated by Eratosthenes'experiment, our school calculated the earth circumference with the help of modern tecnologies like computer and satellites and using Michalsky's algorithm.
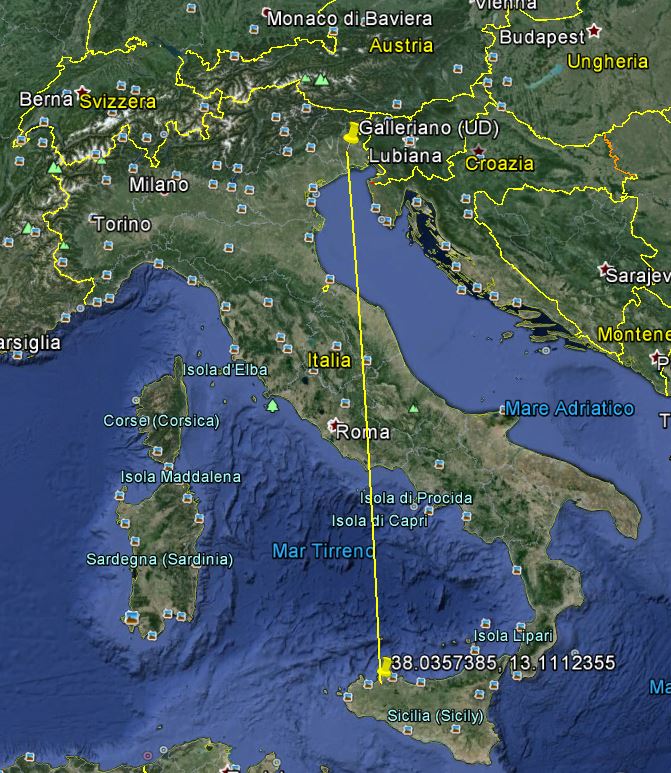
We chose a city on the same meridian of Partinico that is Galleriano, then we calculated the distance from Partinico to Galleriano using Google Earth (880,65 Km).
We used then, Michalsky's algorithm[1] to calculate the solar rays inclinations both in Partinico and Galleriano.
Coordinates:
Partinico:38.0357385. 13.1112355
Galleriano:45.94478890. 13.1202
