The main purpose of this assignment is to understand and learn more about one of physics’ remarkable phenomena, black holes, and in addition to this, what concepts are used to describe black holes.

There are different kinds of black holes; electrically charged holes, rotating holes, and stationary holes. All kinds have a common structure with a singularity at the heart of a black hole and an event horizon surrounding it.

The Schwarzschild black hole is a simple one that does not spin, and has no electric charge. It consists of one event horizon and one singularity.

 

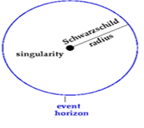
The Schwarzschild black hole. The black dot in the center is the singularity, the blue circle is the event horizon, and the distance between them is called the Schwarzschild radius.

 

A singularity is the mass of the entire star that has collapsed into a single point in space with an infinite density.

The event horizon is the limit of no return where the escape velocity is just equal to the speed of light.

If something falls into a black hole, the only way to escape from it is to overcome its strong gravity by moving away with the so-called escape velocity. In black holes, the escape velocity is higher than the speed of light because it has an extremely strong gravitational field, which means that even light cannot escape a black hole (after it passed its event horizon). And because nothing can travel faster than the speed of light, nothing else can escape a black hole either. The formula that is used to calculate the escape velocity is: 

V is the escape velocity, m is the mass of the object, r is the distance between the black hole and the object, and G is the gravitational constant 6,673∙10^-11Nm²kg^-2

The distance between the center of a black hole, the singularity, and its event horizon is known as the Schwarzschild radius. If the whole mass of a body is inside its Schwarzschild radius, then it is considered a black hole. To calculate the length of the Schwarzschild radius of an object we use the same formula that is used for the escape velocity, but we replace v with the speed of light c=299 792 458 ms^-1. The formula of the Schwarzschild radius is:

By using it we can compute the Schwarzschild radius of any object, for instance our earth. If we replace the mass of the earth which is 5,972∙10²⁴kg we can find out that the Schwarzschild radius of the earth is 8,868∙10^-3m, which means if the earth would shrink until its radius becomes less than 1 cm, the earth would turn into a black hole.