In 205 B.C., the Greek astronomer Eratosthenes, at the time Director of the Great Library of Alexandria in Egypt, proposed a purely geometrical method to measure the length of the Earth's meridian (circle passing through the poles).
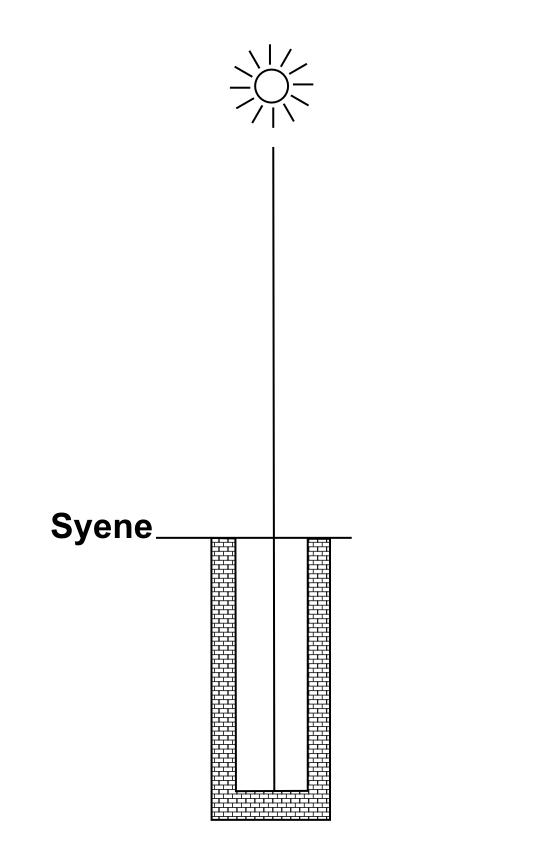
He started by using the observation of shadows made at two different places, Alexandria and Syene (now Aswan) distanced approximately 800 km apart (distance estimated in relation to the time taken by a caravan of camels to connect the two towns !) at the time of the Summer solstice and at noon local solar time.
On that date and at that precise time in the northern hemisphere, the Sun reaches its highest position in the year above the horizon. However, Eratosthenes noticed differences from one place to another.
 |
|
 |
In Syene (approximately situated on the tropic of Cancer) the Sun is at the vertical, so much so that its rays reach the bottom of a well: and the shadows of vertical objects are perfectly centred round them. |
|
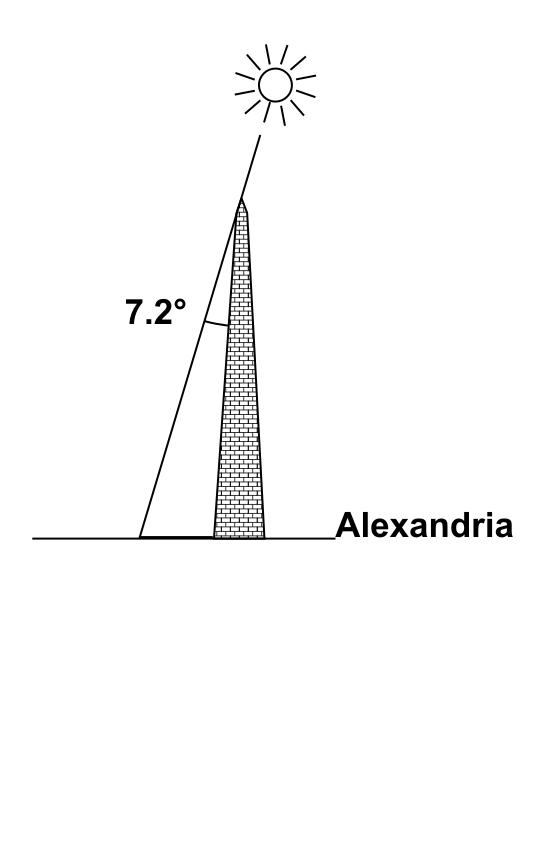
In Alexandria, on the other hand, the Sun is no longer at the vertical, and these same objects have a very shallow offset shadow. Eratosthenes set about measuring the shadow of an obelisk whose height he knew, and used this information to deduce the angle of the sun's rays from the vertical: he found 7.2° |
On the basis of these observations, two hypotheses lay before him:
 |
|
 |
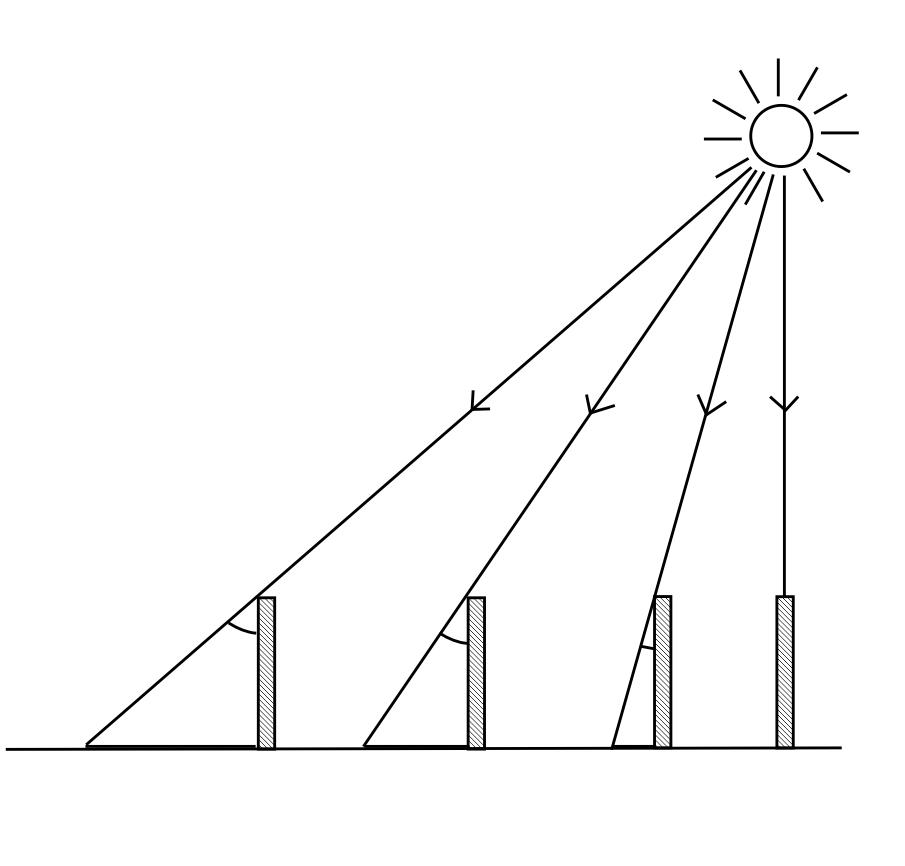
The Earth is flat, but in this case the Sun would be sufficiently close for there to be a significant divergence in its rays reaching distant objects: since objects of identical length have shadows of different length and no shadow at all when vertically underneath the Sun (zero angle). |
|
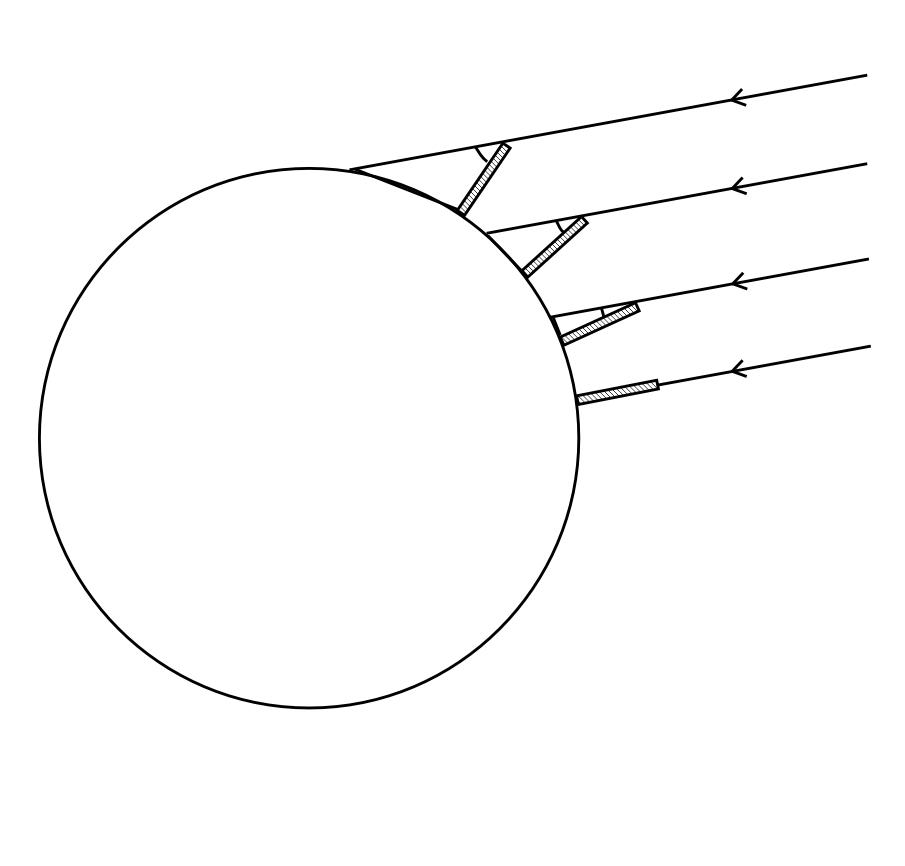
The Earth is not flat, but has a curved, and perhaps even a round surface. Only, the same results can be obtained with sun rays which are all parallel: this implies that the Sun is sufficiently far away, very, very far away… |
Eratosthenes opted for the second hypothesis. Indeed, the Ancients had already suspected that the Earth was not flat, on the basis of various observations seemingly providing evidence that its surface was somewhat curved: navigators perched on the top of their main mast are the first to perceive the distant coastline; observers on top of a cliff have a longer view of ships moving towards the horizon than observers on the beach; the pole star is not at the same height above the horizon in Greece as in Egypt; finally during eclipses of the Moon, the shadow of the Earth projected onto the Moon shows a circular section.
Convinced that the Earth is round, our genius Eratosthenes set about tracing his famous "amazingly simple" geometrical figure, which he used to calculate with ease the length of the Earth's meridian! Look for yourselves:
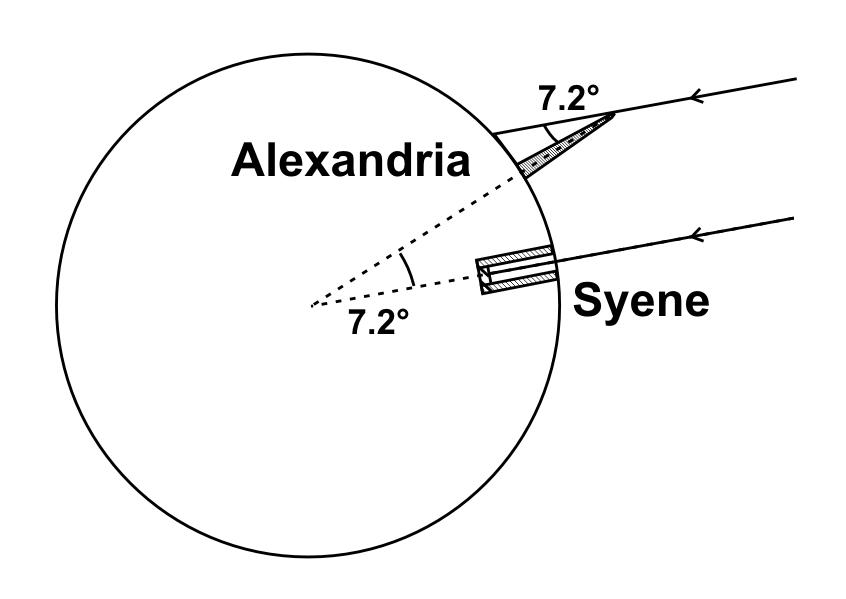
If the Earth is round, by extending the vertical in Alexandria (the obelisk) and the vertical in Syene (the well), these two verticals should by definition meet at the centre of the Earth. Also, Eratosthenes knew that the town of Syene being situated directly South in relation to Alexandria, the two cities were situated on approximately the same meridian. Since the sun's rays are indeed parallel, the angle formed by the two verticals at the centre of the Earth must therefore be identical to the angle he measured with the shadow of the obelisk (7.2°).
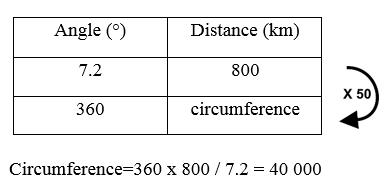
The proportion of this angle in relation to the 360° of a circle is the same as the proportion of the distance separating the two cities (approximately 800 km) relative to the circumference of a circle (in this case the Earth's meridian). The rest you can guess: 360° divided by 7.2° gives 50, and 800 km multiplied by 50 indeed gives 40000 km (a length which was found again later but using other methods).