Project 5: Same polygons with different circles and a surprise (GER, RO, IT, CRO) 

• Worksheet  and creative, common results (GER)

• Looking for help from a student (GER) -> see here .
• Student Sophia from Romania has sent it. Thank you! So we can now work on this project!

You can change the settings here to get english subtitles!

Continuations:

• Finding the number of different carvings for pentagons, hexagons, ...
• How many arrangements of triangles in a pentagon, hexagon, ... ?
• Is there a formula for the number of different carvings?
• Proof for pentagons, hexagons, ...
• The circles could be animated at the end e.g. by rotation
   
• Construction on paper (CRO)

German students will talk about your work next week and give some comments in the Forum!

• Proof of Japanese Theorem from Italian students first part: 

A triangle is always cyclic. Let's prove the Japanese theorem, dividing it into parts. Let's start from "One and only one circle passes through three given non-collinear points" . and that these three points are even the vertices of a unique triangle. Let's explore some of the properties: the incenter and the incircle of the triangle and the inradius and the area.

• Second Part:

The circumcenter is the point where the perpendicular bisectors of a triangle intersect. The circumcenter is also the center of the triangle's circumcircle - the circle that passes through all three of the triangle's vertices. Let's explore the relation between the area of ABC the inradius and circumcenter.

• Third Part

Carnot's Theorem and Japanese Proof

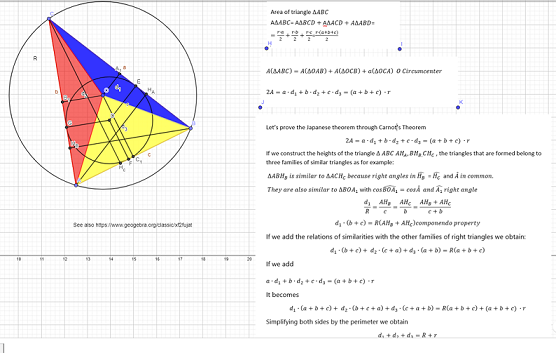
• Proof of  the Japanese Theorem through iteration by Norma Lisa Neiman 

Carnot's Theorem

Explaining through Carnot’s Theorem the Japanese Theorem.by Norma Lisa Neiman