You will be conducting this experiment paired with another class (whose particulars we will be forwarding to you) but you will not need either an obelisk or a well! All you will each need is a simple vertical stick, preferably of identical height to simplify comparisons of shadow measurements.
| 
| 
| 
|
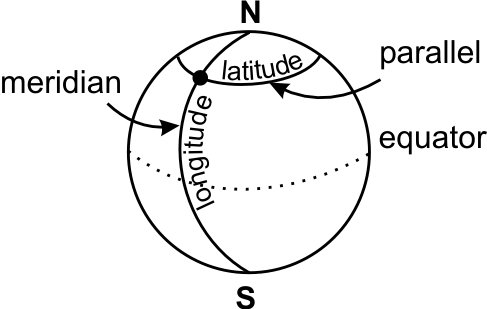
| It will not be necessary either for one of the two partners to be positioned on the tropic of Cancer! It need only be located at a distinctly different latitude to the other. | If the two schools are located on more or less the same meridian, well and good… Otherwise there will be no problem since each one in turn will "see things differently" with noon-time being different on each one's meridian! | It is not the number of kilometres between your two schools which will be taken into account, but the shortest distance separating the two parallels giving your latitudes (you will see that this distance is easy to calculate). |
No need either to wait for the Summer solstice before taking your measurements! Any day of the year may be used provided that it is the same day chosen by your partner: it would be wise therefore to come to agreement with your partner and to repeat the "practical" on a certain number of days …
As for each partner's determination of midday at local solar time (different from one place to another and on every day of the year) no problem either: all you need do is to identify the shortest shadow during the half hour either side of 13 h winter time : kid's stuff… Provided of course that the Sun makes an effort!
Example of two classes located in Lafrançaise (France) and Meerut (India)
Thursday 10 February 2011.
The coordinates of the two towns:
Lafrançaise: latitude 44°08'N, longitude 1°15'E
Meerut, latitude 29°00'N, longitude 77°42'E.
With these measurements the children are able to calculate the angle of the Sun's rays (at midday local solar time), accurate to half a degree, using a very simple geographical figure
For Lafrançaise they find alpha 1 = 58.5°
And for Meerut alpha 2 = 43.5°.


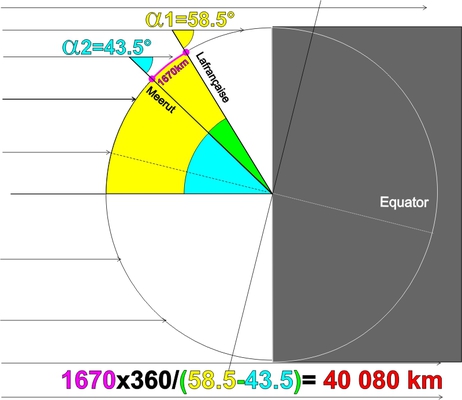

| But how is it possible, using these two angles to calculate the famous alpha angle? You need only subtract alpha angle 2 from alpha angle 1, which gives 15°. | | Since the two partnered schools are not positioned on the same meridian, the shortest distance must then be determined between the parallel of Lafrançaise and the parallel of Meerut. This is very easy: on a map, a careful tracing is made of the two parallels and, using the map scale, the distance between them is calculated. Here the value found is in the order of 1670 km. |

We now have in hand the two elements needed to calculate the Earth's meridian using "Eratosthenes' method": the alpha angle of 15° and the distance of 1670 km between the two parallels. The proportion of a whole circle relative to the result of 15° being 24 times (360° divided by 15°), the meridian is calculated by multiplying 1670 km by 24, which indeed gives 40080km….An efficient method, provided that the measurements are as precise as possible (especially if the latitudes are nearer to one another !).
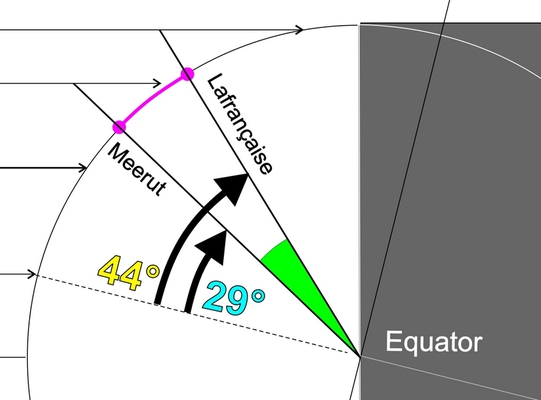
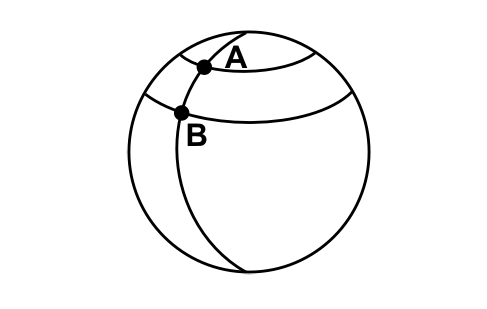
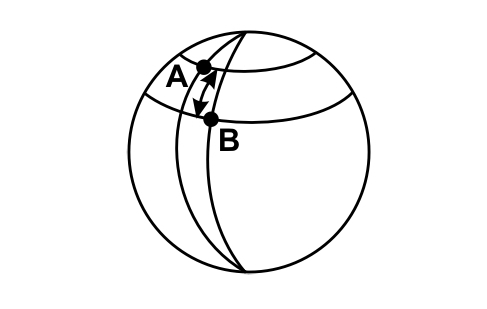
It is interesting to note, as shown in figure, that the difference between the two latitudes gives the famous alpha angle immediately! With our two partnered schools, this gives:
44°08'-29°00'=15°08'. We note that the measurements made by the children are very accurate since our school friends deduced an angle of 15°, which was therefore very close.
We stress the fact that the "direct method" for calculating the alpha angle using knowledge of the two latitudes must absolutely not be given to the children at the outset! On the other hand, it could be useful to them, at a later stage, to detect any possible errors in their measurements…