ELLIPSE

A curved line forming a closed loop, where the sum of the distances from two points (focus) to every point on the line is constant. The standard equation of the ellipse in the cartesian plane is:

We can also say that, an ellipse is a curve on a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve. As such, it is a generalization of a circle, which is a special type of an ellipse that has both focal points at the same location. The shape of an ellipse (how 'elongated' it is) is represented by its eccentricity, which for an ellipse can be any number from 0 (the limiting case of a circle) to arbitrarily close to but less than 1.                                                                       

                                                                                         

 

Definitions:

Major/minor axis: the longest and shortest diameters of an ellipse.

Semi-major axis: The longest radius of an ellipse.

Semi-minor axis: The shortest radius of an ellipse.

Foci (Focus points): The two points that define the ellipse.

 

Mathematical relations:

If  AB > CD (see the figure above)

major axis = A,A1                       PF1 + PF2 = AA1(2a)            a2= b2+c2

minor axis = B,B1                       focal = F,F1

Eccentricity: 

                                                                         

 

 

If   CD> AB

The ellipse is longer on y direction and shorter on x direction

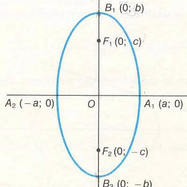
major axis = B1B2                       PF1 + PF2 = B1B2=2b            b2=a2+c2

minor axis = A1A2                       focal = F1,F2

Eccentricity: