POWERS OF 10
RULES
POWERS’ PROPERTIES

POWERS WITH A NEGATIVE EXPONENT
How can we solve such an expression?
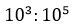
In two ways:
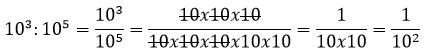
Or, using properties:
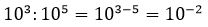
So we have introduced the powers with a negative exponent.
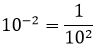
If we change the sign of the exponent we move the power of ten from the numerator to the denominator.
Even in this case, we have the same rules as before but take attention:

CHANGE A NUMBER IN A POWER OF TEN
Let’s see two examples.
345.000.000.000.000.000.000
0,00000000000078
- I write the number with a comma after the first figure different from zero
- The exponent of 10 must be equal to the number fo figures:
- That you have after the first figure (in our example the figure 3) if the number is bigger than one and it has got a positive exponent.
- That you have before the first non-zero figure (in our example the figure 7) if the number is smaller than one and it has a negative exponent.
In our first example, the number has got 18 zeros, the figure 5 and the figure 4. So:
3,45 x 1020
In the second example, before the figure 7, we have 13 zeros (including the one before the comma). So:
7,8 x 10-13
EXERCISES
Try to transform these numbers using the powers of ten.
0,00000000000000506
23.070.000.000.000.000.000.000
0,0000057
2,000008
8.600.500.000.000.000
UNITS OF MEASURE
|
zetta
|
exa
|
péta
|
téra
|
giga
|
méga
|
kilo
|
1
|
milli
|
micro
|
nano
|
pico
|
|
1021
|
1018
|
1015
|
1012
|
109
|
106
|
103
|
100
|
10-3
|
10-6
|
10-9
|
10-12
|
|
Zm
|
Em
|
Pm
|
Tm
|
Gm
|
Mm
|
km
|
m
|
mm
|
µm
|
nm
|
pm
|
EXERCISES
Transform in the requested Unit of Measure and, at the end, express the result using the powers of 10.
34.500.000 Pm = ………………………………………………….km
2.170.000.000.000 µm = ……………………………………..km
345.070.000.000.000.000 pm = ………………………….m
0,405 Zm =……………………………………………………………..m
0,0000057 mm = ………………………………………………….nm
2,08 Tm =……..……………………………………………………..mm
8.600.500.000.000.000 m = ………………………………..Tm
THE EXPONENTIAL LAW
Take a sheet from your exercise book. Fold it in half . Then fold it again. Go on…how many times can you fold it?
If you have solved this little exercise, maybe you begin to understand what exponential growth means. (with 10 as base of the power the growth is very faster).
Let’s solve another problem.
A man has won a TV quiz game. The showman tells him to choose between two prizes:
- The prize A is 1 million of Euros
- The prize B is 1 Euro for the first day of the year, 2 euros for the second day, 4 euros for the third day and so on…until the 31st of January
Which prize should you choose?
If you don’t understand, please look at this video explaining what can happen with exponentials. https://www.youtube.com/watch?v=KnQZ3Mg6upg
PROBLEM 1
The city of Boulder (USA) in 1950 had 20.000 inhabitants.
From 1950 to 1970, every year the population of the city has grown by 6%. How many inhabitants did the city have in 1970?
Going on with this growing percentage, how many inhabitants should the city have today?
PROBLEM 2
At 11.00 am, in a bottle in the science laboratory, the doctor Morgan put a Bacterium, that can reproduce itself in an asexual manner. Every minute the Bacteria population has doubled. If at 12.00 am, the bottle is completely full of Bacteria, at what time wasthe bottle half full?
THE SCIENTIFIC NOTATION
When you work with science, you should have to manage very little numbers (for example the dimension of an electron) or very big numbers (for example the distance from the Earth to Proxima Centauri, the nearest star outside the Sun System).
To avoid numbers with a large number of zeros, scientists have thought to use powers of ten.
So, if you use the meter as the reference unit of measure, you have:
- Positive power for objects bigger than a meter
- Negative power for objects smaller than a meter
EXAMPLES
Dist. Earth-Proxima Centauri = 40141900000000000 m = 4,01419 x 1016 m
Classical Electron ray = 0,0000000000000028179 m = 2,8179 × 10−15 m
ATTENTION: in some calculator devices, you should find this:
4,01419e+16
It means (the “e” means exponential; the base is 10 and it is implied).
4,01419 x 1016
The name of this manner of express numbers is Scientific notation.
The real advantage of scientific notation is:
- To immediately understand which the order of magnitude of an object is (how many figures we must use for describe it).
- We can compare in an easy manner the dimension of two different objects.
ATTENTION: as you can see from the previous examples, it’s very important that the order of the number preceding the power is the unit (Ex: 4,01419), otherwise it should be very difficult to campare two numbers expressed in the scientific notation.
EXERCISES
How many digits these numbers are made of?
2 x 108
7,0546 x 1013
234,097 x 1012
6,96 x 10-4
4,01419e+16
COMPARE. Which is the biggest one?
|
1,02 x 106
|
9,98 x 105
|
|
5,2 x 10-6
|
6,96 x 10-4
|
|
7,0546 x 1013
|
234,097 x 1012
|
|
235,2 x 10-11
|
1,07 x 10-10
|
|
0,0511 x 1018
|
111,01 x 1015
|
|
1,2 x 106 m
|
3,31 x 108 km
|
Link any example with his dimension.
|
EXAMPLES
|
DIMENSION
|
|
Andromeda Galaxy (diameter)
|
970 nm
|
|
A Mosquito
|
1,164 x 107 m
|
|
Fuji Mount
|
2,366 x 1021 m
|
|
Saturn (diametere)
|
3,776 km
|
|
Ebola Virus
|
0,007 m
|
|
Blood cell
|
0,000000825 m
|
LIGHT YEAR
When you work with very big distances, we can use another unit of measure, that is not a multiple of the meter, instead of using powers of ten: the light year!!
The light year is the distance that light can cover in one year.
The light speed is 300.000 km/s; so to understand how many kilometers the light can do in one year, we have to know how many seconds there are in one year.
|
N. sec.
|
In 1 minute
|
In 1 hour
|
In 1 day
|
In 1 Year
|
|
|
60
|
60x60 = 3600
|
3600 x 24 = 86.400
|
86.400 x 365 = 31536000
|
So we must multiply this number by 300.000.
1 Light Year = 31.536.000 x 300.000 = 9460800000000 km
9.460.800.000.000 km = 9.460.800.000.000.000 m = 9,4608 x 1015 m
As a conclusion we can look at the previous example:
Dist. Terra-Proxima Centauri = 40141900000000000 m = 4,01419 x 1016 m =
= 4,2 light years à very simple!!!!!!!!!
BIBLIOGRAPHY
Alex Bellos, I numeri ci somigliano