January 2016: French students aged 18 studied an example of fratals, called the snowflake, and discuss how useful fractals are for our daily life.

Watch the videos of their school oral examination and answer the following questions. All videos show the same content which is presented by different students.

1. describe the procedure to draw the geometric diagram of the snowflake.

2. Explain the mathematical formulas used to describe the properties of the snowflake.

3. What is the paradox showed by this snowflake.

4. Extend to the concept of fractals: what is a fractal, what is it useful for in real life?

Thanks for your replies.

Valentin Binet, from France, presents below his understanding of the snow flake task.

March 2016: The Erasmus+ learning meeting taking place in the French school in March 2016 coincides with the Franch national week to celebrate mathematics in schools in France. Math in English teachers all over Normandy are organising in their schools an activity called "the chaos game". Starting from an equilateral triangle and a die, visitors are asked to roll the die and depending on the number shown face up, they are invited to spot a point in the traingle. Once a large number of visitors have contributed with their points, what we expect to be chaos turns out to give a very organised diagram although it is based on randomly thrown die. How surprising!

French and Bulgarian math teachers collaborate together on this activity opened to a wide audience in the school.

 

April 2016: The visit of the Bulgarian students in France coincided with the Chaos game In Normandy.

Bulgarian students aged between 16 and 17 years from the 10a class with the help of Ms. Ruseva examined the result of the game by making computer programs. The choice of a starting point is random. The programs generate random numbers from 1 to 6 after which the rules of the game are executed. In the work process were needed not only computer skills, but also a lot of mathematical knowledge – calculating coordinate points, division of a segment in a given ratio, etc. The result was incredible, but one after another questions rose up.

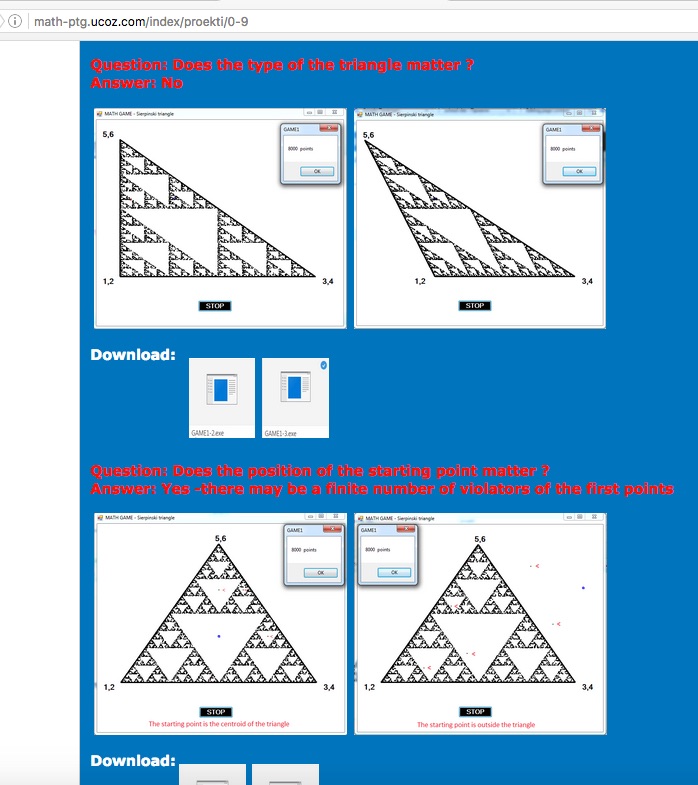
1. Does the type of the triangle matter?

2. Does the position of the starting point matter?

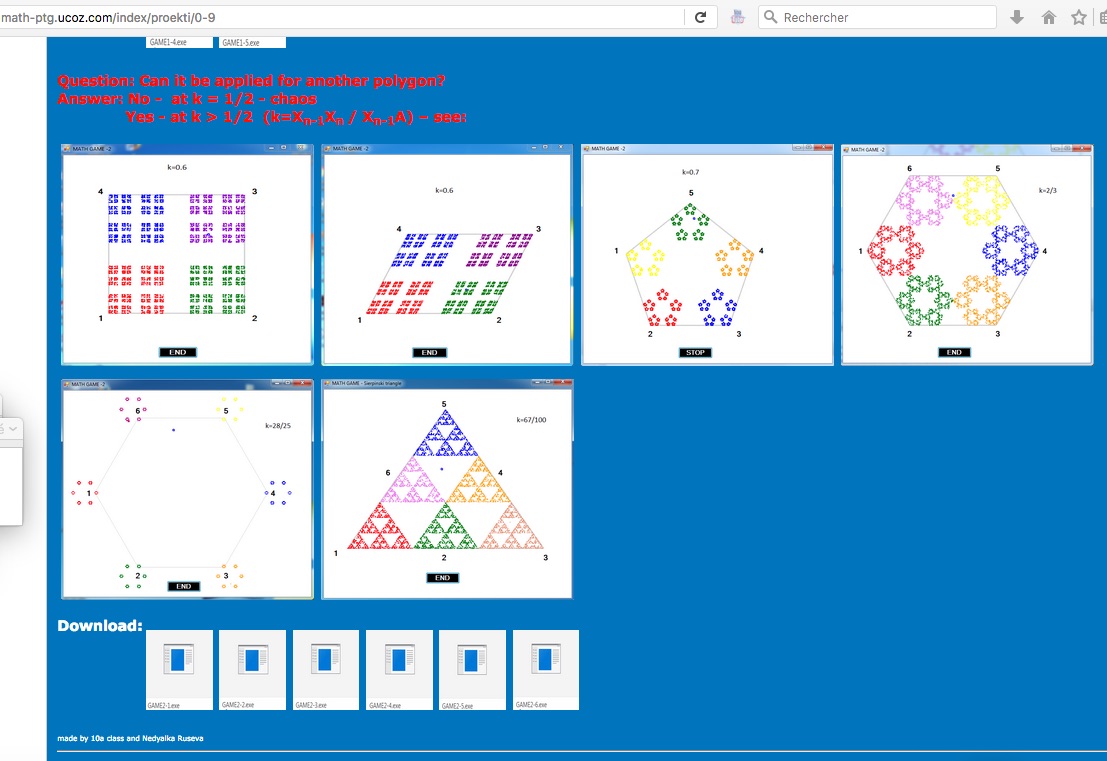
3. Can it be applied to other polygons?

Answering the last question, in the beginning we were disappointed, because nothing seemed to work out, but the math teacher recommended looking for information on the internet. We found a lot of information about the fractals, which unfortunately we do not study at school.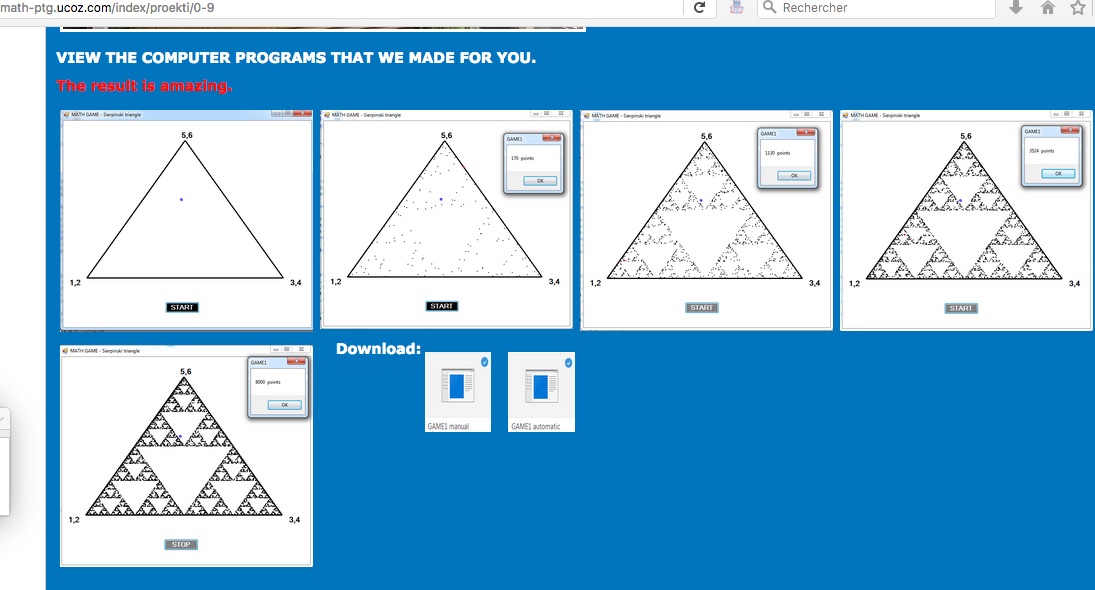

A lot of interesting things happened. Take a look : Chaos game